Сообщений в теме: 180

[kozlov]

Коротенькое введение. Для тех, кто забыл математику. Если мы возьмем пистолет и начнем стрелять по мишени, то часть пуль попадет в десятку, часть в девятку, а еще в восьмерку и так далее. Теперь подсчитаем количество попаданий. Допустим, в 10 Вы попали 400 раз, в 9 — 300, в 8 — 250, в 7 — 200 и т. д.

Отложим по оси ординат (Y) — очки, а по оси абсцисс (Х) — количество попаданий. Мы получим такую картинку:

 Gaussian0.jpg   44.1К   1 скачиваний



Если разделить мишень пополам вертикальной чертой и посчитать для каждой половинки количество попаданий, картинка зеркально отобразится, получится такая вот колоколообразная кривая:


 Gaussian1.jpg   52.67К   43 скачиваний



Она называется Кривая нормального распределения, или гауссиана.
Закон нормального распределения в природе встречается чаще всего. В этом легко убедиться, насыпав горку песка — в идеале любое ее сечение будет сильно напоминать наш колокол. Можно кидать игральные кости, монеты, что угодно — получится все равно такой же колокол. Ну а наш построенный колокол дает вероятность того, что стрелок попадет в 10, 9, 8 и т. д.

Кривые могут быть пологими и крутыми. Для нашего примера синяя кривая бодет соответствовать метком стрелку (у него больше попаданий в десятку), а желтая — мазиле:






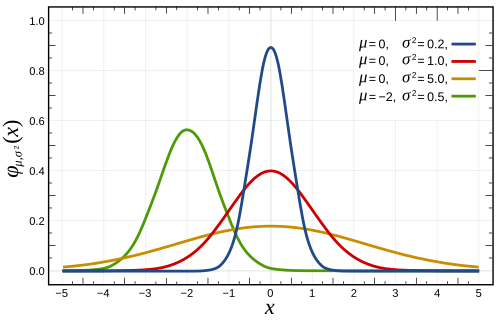
Но заметьте важную деталь — все кривые — совершенно четко куполообразные!

Что бы Вы ни делали, что бы ни подбрасывали, а любая величина просто обязана подчиняться нормальному распределению, если на нее воздействуют случайные помехи. Если свойства укладываются в такой колокол - это нормально. Если колокол кривой — это значит только одно: процесс случайностей претерпел вмешательство, его кто-то искусственно подправил.

Ну а теперь перейдем собственно к выборам.
Перед нами — официальный график прохождения выборов.
 000tzr59.jpg   123.42К   63 скачиваний
график взят отсюда: http://oude-rus.livejournal.com/542295.html

[K.Serg]

...одаренные интеллектуально председатели избирательных комиссий, рисовали круглые цифры, подгоняя результат к ней, чтобы отрапортовать начальству: у нас, мол, 70%, ну, или 60%. кому что велели...

А это про "неодаренных"...
http://news.rambler.ru/12075891/

Сообщение отредактировал K.Serg: 08 December 2011 - 16:00

[kozlov]

А это про "неодаренных"...
http://news.rambler.ru/12075891/

Это все можно оспорить. Колокол же неоспорим

[destructor]

Колокол же неоспорим

Почему он не оспорим? Из графика по выборам можно сделать вывод - Чем больше график похож на купол, тем более случаен был выбор этого кандидата. Пологий склон в право указывает на широкий разброс по регионам (это нормально и это так). Крутой левый склон указывает на то, что почти нет регионов без поддержки вообще.

Обратите внимание, что у коммунистов тоже некое искажение, но всеже есть куполообразность. Это потому, что какаято часть выбирающих голосовало осознано за них (убежденные сторонники) и они исказили купол, но большая доля случайно (лишбы не ЕР).

ЗЫ Я голосовал за КПРФ и мой голос добавил куполообразности, потому что я мог проголосовать и за Яблоко .

Сообщение отредактировал destructor: 08 December 2011 - 16:52

[kozlov]

Почему он не оспорим? Из графика по выборам можно сделать вывод - Чем больше график похож на купол, тем более случаен был выбор этого кандидата. Пологий склон в право указывает на широкий разброс по регионам (это нормально и это так). Крутой левый склон указывает на то, что почти нет регионов без поддержки вообще.

Обратите внимание, что у коммунистов тоже некое искажение, но всеже есть куполообразность. Это потому, что какаято часть выбирающих голосовало осознано за них (убежденные сторонники) и они исказили купол, но большая доля случайно (лишбы не ЕР).

ЗЫ Я голосовал за КПРФ и мой голос добавил куполообразности, потому что я мог проголосовать и за Яблоко .

Чем более случаен выбор - тем более пологий колокол. Посмотрите на желтый колокол в заходном посте. Искажения купола возможны только в том случае, если в процесс на ходу вмешивалась сторонняя сила. Без вмешательства колокол будет симметричный, это закон математики, ничего не поделать. Можете проверить его, бросая монетки или кубики - получите все тот же колокол.
Из случайных чисел неизбежно получается колокол. А вот если начать мухлевать с кубиком и ставить, например, каждый третий бросок шестеркой вверх - Вы получите Колокол с кривым плечом
Особенно ярко это виден вброс по зубцам возле круглых цифр.

А времени в этом графике и нет... здесь - количество участков.

Сообщение отредактировал kozlov: 08 December 2011 - 17:15

[destructor]

Чем более случаен выбор - тем более пологий колокол. Посмотрите на желтый колокол в заходном посте. Искажения купола возможны только в том случае, если в процесс на ходу вмешивалась сторонняя сила. Без вмешательства колокол будет симметричный, это закон математики, ничего не поделать. Можете проверить его, бросая монетки или кубики - получите все тот же колокол. Из случайных чисел неизбежно получается колокол. А вот если начать мухлевать с кубиком и ставить, например, каждый третий бросок шестеркой вверх - Вы получите Колокол с кривым плечомОсобенно ярко это виден вброс по зубцам возле круглых цифр.А времени в этом графике и нет... здесь - количество участков.

Пример со стрелком , по моему, неудачен. Давайте предположим что на каждом участке люди по очереди оказываются в середине круглой комнаты с несколькими дверьми вокруг. Одна дверь хорошо известна(ЕР), вторая когдато была достаточно известна (КПРФ), остальные безликие. Задача выбрать дверь для выхода. Люди желающие войти в "известную дверь" - пойдут именно туда и случайности тут никакой. Другие, не желающие по каким либо причинам идти в эти двери, будут выбирать между остальными. Определеная часть войдет в "известную когдато", а вот остальные поделяться меж оставшимися безликими и чем больше людей, тем точнее они разделяться (крутые пики графика). Далее если эти комнаты расположены в разных местах обитания с разным образом мысли, то отличаться они будут только процентом людей входящих в изветные двери(пологий склон), а распределение между оставшимися будет точно такимже.
Понятно, что другие двери не вполне безлики и потому пики будут отличаться.
А на счет "зубцов" - тут я полностью согласен(хотя при дискретности в 0.5%...) . Там чтото не так. И еще подьемчик в районе 100% - это явно "феодальные" регионы .


ЗЫ кстати - осознаный выбор это какраз и есть "внешняя сила" изкажающая случайность

Сообщение отредактировал destructor: 08 December 2011 - 18:17

[WHEEL]

А как бы выглядел график идеальной партии, за которую проголосовало бы всё население?

[destructor]

А как бы выглядел график идеальной партии, за которую проголосовало бы всё население?

Точка в правом верхнем углу ))

[destructor]

нет... это былабы линия идущая сначала по оси Х переходящая в максимум на ста процетнах.

[kozlov]

А как бы выглядел график идеальной партии, за которую проголосовало бы всё население?

вертикальная прямая у цифры 100

[kozlov]

Пример со стрелком , по моему, неудачен. Давайте предположим что на каждом участке люди по очереди оказываются в середине круглой комнаты с несколькими дверьми вокруг. Одна дверь хорошо известна(ЕР), вторая когдато была достаточно известна (КПРФ), остальные безликие. Задача выбрать дверь для выхода. Люди желающие войти в "известную дверь" - пойдут именно туда и случайности тут никакой. Другие, не желающие по каким либо причинам идти в эти двери, будут выбирать между остальными. Определеная часть войдет в "известную когдато", а вот остальные поделяться меж оставшимися безликими и чем больше людей, тем точнее они разделяться (крутые пики графика). Далее если эти комнаты расположены в разных местах обитания с разным образом мысли, то отличаться они будут только процентом людей входящих в изветные двери(пологий склон), а распределение между оставшимися будет точно такимже.
Понятно, что другие двери не вполне безлики и потому пики будут отличаться.
А на счет "зубцов" - тут я полностью согласен(хотя при дискретности в 0.5%...) . Там чтото не так. И еще подьемчик в районе 100% - это явно "феодальные" регионы .

ЗЫ кстати - осознаный выбор это какраз и есть "внешняя сила" изкажающая случайность

Вы сильно усложняете задачу, а она и без того непростая.
Проведите такой эксперимент: возьмите 20 монет и бросьте их на стол, скажем, раз 20, а лучше 50. Всем "орлам" присвоим 0, всем "решкам" - 1. У Вас получатся разные значения, но чаще всего будут выпадать числа, близкие к 10. И чем больше бросков Вы сделаете, тем ближе к колоколу будете получать график. В середине будет 10, слева 0, справа - 20. Максимум колокола будет на 10. Это закон природы, альтернативы ему нет.
На графике с выборами - та же песня. Многие миллионы людей голосовали в десятках тысяч участков. Ясно, что в этой каше будет именно случайное распределение, несмотря на то, что каждый человек делал осознанный выбор. На участке Х - одна раскладка по партиям, на участке Y - другая, на участке Z - третья. Вот они-то и должны построить классический колокол. И чем сильнее кривая будет отличаться от колокола - тем больше было махинаций.
Все просто...

[ars1117]

БРАВО!

Не менее любопытно, что верхушка колокола ЕдРа, если ее экстраполировать, стремится к 30-35%. Это и есть примерно «честная цифра» проголосовавших за ЕдРо. Все равно — больше всех. Можно было и не вбрасывать и не мухлевать!

ДА! Но тогда Едро получило бы меньше мондатов!

[Жорик Л.]

Ну так.

Тихомиров "подал в отставку" с поста председателя местного отделения ЕР . Пока .

[Жорик Л.]

И чем сильнее кривая будет отличаться от колокола - тем больше было махинаций. Все просто...

А военнослужащие ?
Сначала Дальневосточнйй ПО и Тихоокеанский Флот - все "как по команде" голосуют за ЕР - резкий старт . Далее затишье до Читы-Иркутска .
В Западной Сибири , кроме "стройбата" ничего нет . Потом Уральский ВО , Московский и Ленинградский с Сев-Западным ПО и флотами Балтийским и Северным .
Вот вам и "всплески" . Какое кол-во голосующих по команде ? Да ещё организованно-одновременно .

Сообщение отредактировал Жорик Life: 08 December 2011 - 22:36

[ars1117]

А военнослужащие ?
Сначала Дальневосточнйй ПО и Тихоокеанский Флот - все "как по команде" голосуют за ЕР - резкий старт . Далее затишье до Читы-Иркутска .
В Западной Сибири , кроме "стройбата" ничего нет . Потом Уральский ВО , Московский и Ленинградский с Сев-Западным ПО и флотами Балтийским и Северным .
Вот вам и "всплески" . Какое кол-во одновременно голосующих по команде ?

Сейчас сроки службы небольшие(1 год). И за это время сделать из солдата зомби не получится. "Он вышел родом из народа..."(солдат).

[kozlov]

ДА! Но тогда Едро получило бы меньше мондатов!

Зато без массового недовольства и митингов

[kozlov]

А военнослужащие ?
Сначала Дальневосточнйй ПО и Тихоокеанский Флот - все "как по команде" голосуют за ЕР - резкий старт . Далее затишье до Читы-Иркутска .
В Западной Сибири , кроме "стройбата" ничего нет . Потом Уральский ВО , Московский и Ленинградский с Сев-Западным ПО и флотами Балтийским и Северным .
Вот вам и "всплески" . Какое кол-во голосующих по команде ? Да ещё организованно-одновременно .

Здесь нет времени, здесь... График показывает проценты и участки.
Вот смотрите. Коричневая кривая. Зубчик 50%. Смотрим вниз, на ось Х, видим 50%. Смотрим влево, на ось Y, видим 1000 участков. Это значит, что за весь день голосования в 1000 участков ЕР набрала 50% голосов. Эти 1000 участков разбросаны по всей территории России.
20% ЕР набрала в 200 участках. И 100% - в 650 участках (это вообще непонятно - никто больше не пришел?).

Поэтому-то колокол должен быть правильным, как у остальных партий.

Опять же никакой флот не может объяснить зубцы возле круглых процентов. Почему 60% ЕР набрала в большем количестве участков, чем 59% и 61%? То же самое касается 65, 70, 80, 90 и т.д. процентов. Эти зубцы ничем, кроме подгонки под нужную цифру, объяснить невозможно.
Но гораздо более сильный аргумент - конечно,сам колокол, вернее, его отсутствие. Правое его пологое плечо необъяснимо ничем, кроме вмешательства, то есть махинаций

[destructor]

Вы сильно усложняете задачу, а она и без того непростая.Проведите такой эксперимент: возьмите 20 монет и бросьте их на стол, скажем, раз 20, а лучше 50.

А Вы слишком упрощаете - используете слишком простую функцию для моделирования . Подкидывание монет это чисто случайность. Еще раз скажу - В нашем случае случайность только отчасти и присутствуют не случайные а осознаные факты - выбор, вброс, пропаганда, принуждение . Чем дальше от больших городов, тем выше процент за номинального кандидата. Правильнее будет с монетами - бросать эти монеты в разные ящики на выбор. Ктото кидает в конкретный, заведомо выбраный ящик, а ктото в случайном порядке раскидывает.

Сообщение отредактировал destructor: 09 December 2011 - 08:10

[kozlov]

А Вы слишком упрощаете - используете слишком простую функцию для моделирования . Подкидывание монет это чисто случайность. Еще раз скажу - В нашем случае случайность только отчасти и присутствуют не случайные а осознаные факты - выбор, вброс, пропаганда, принуждение . Правильнее будет с монетами - бросать эти монеты в разные ящики на выбор. Ктото кидает в конкретный, заведомо выбраный ящик, а ктото в случайном порядке раскидывает.

Так ведь я не зря говорю про монетки. Вы попробуйте. Получите классический колокол, а потом начните "подыгрывать", скажем, "решке", при каждом бросании переворачивая 4-5 "орлов". И Вы получите колокол ЕР.
Случайность, повторю, в распределении голосов по участкам. У Вас - свой участок голосования, у меня - свой, и никакого осознанного выбора в этом нет. Классический случай нормального распределения.
В конце концов - почему у всех партий нормальный колокол, в точности по законам математики и физики, и только у ЕР - искаженный?

[Витал]

Колокол же неоспорим

Чем более случаен выбор - тем более пологий колокол

Вот именно. При случайном голосовании. Но ведь оно не случайное, ведь так? Так почему же должен быть именно колокол?
Возьмите Штаты. Там две партии (упрощённо). Есть штаты, поддерживающие ту или другую партию, но в целом по стране тоже не будет никакого колокола.

[Fantomas]

Правда я не понял при чем тут выбора и распределение случайных величин?

[35688]

Опять же никакой флот не может объяснить зубцы возле круглых процентов. Почему 60% ЕР набрала в большем количестве участков, чем 59% и 61%? То же самое касается 65, 70, 80, 90 и т.д. процентов. Эти зубцы ничем, кроме подгонки под нужную цифру,

Квантовая механика может )))) - это "энергетические уровни".... (Хотя подгонять результат под круглый процент - это идиотизм, такой же, как покупка красивых номеров на машину)

А ненормальность распределения голосов за ЕР - это свидетельство того, что голосовавшие за эту партию живут в ненормальном пространстве или относятся к другому классу граждан... (напрмер с нулевой массой и нулевыми потребностями, но с правом голоса...)

[K.Serg]

Это все можно оспорить. Колокол же неоспорим

Что оспорить? Увольнение руководителей?!

[kozlov]

Вот именно. При случайном голосовании. Но ведь оно не случайное, ведь так? Так почему же должен быть именно колокол?
Возьмите Штаты. Там две партии (упрощённо). Есть штаты, поддерживающие ту или другую партию, но в целом по стране тоже не будет никакого колокола.

Выбор каждого конкретного человека может быть и случайным и осознанным. Когда речь идет о миллионах избирателей - всегда получается случайное разбиение по участкам.
Вот смотрите. Каждый прохожий идет по улице с какой-то неслучайной целью: кто в магазин, кто на работу, кто домой, кто просто гуляет. Но когда Вы идете по той же улице, то встречаете их в совершенно случайной последовательности. В этом все дело.
А колокол будет в любой стране при выборах. Причем чем честнее, тем более ярко выраженный колокол получится, это так же верно, как если на один участок пришло 400 чел, а на другой 600, то всего на два участка пришло 1000. То и другое - и 1000, и колокол, чистой воды математика. Не получится при сложении 400 и 600 ни 999, не 1001, а получится 1000. При случайном разбиении избирателей по участкам - получится колокол.
Посмотрите - там в заходном тексте есть ссылка на страничку, где описана математика процесса.

[kozlov]

Правда я не понял при чем тут выбора и распределение случайных величин?

Все просто. Нет участков для выборов в конкретную партию. Избиратель идет голосовать по месту прописки. Получается пересечение двух множеств: множество избирателей (каждый со своими предпочтениями) случайно пересекается с множеством участков. То есть на участке собирается случайное число проголосовавших за ту или иную партию. В больших масштабах должен получиться колокол. Да ведь он и получился - у всех, кроме ЕР

Квантовая механика может )))) - это "энергетические уровни".... (Хотя подгонять результат под круглый процент - это идиотизм, такой же, как покупка красивых номеров на машину)

А ненормальность распределения голосов за ЕР - это свидетельство того, что голосовавшие за эту партию живут в ненормальном пространстве или относятся к другому классу граждан... (напрмер с нулевой массой и нулевыми потребностями, но с правом голоса...)

Ну тут же не квантовая механика... Энергетические уровни - штука понятная и объяснимая - в них должно вместиться кратное число длин волн.

Ненормальность распределение - прямое доказательство мухлежа, и более ничего. Это то-чего-не может-быть. Даже в ненормальном пространстве с красивыми номерами.

Что оспорить? Увольнение руководителей?!

Речь о результатах выборов. Оспорить можно любые заявления о нечистоплотности работы участков в любой форме. Колокол оспорить невозможно.

[yuvoront]

Да, Аркадий, очень показательный график. Для меня, как человека с технической и математической подготовкой, никаких слов больше не надо. Все кристалльно ясно из графиков. Единая Россия, нарушив гауссово распределение, тем самым выдало себя с головой. Особенно бросается в глаза скачок с правой стороны кривой гауссианы. Кто же это так задорно рапортовал о 90-100% проголосовавших за ЕР? Врядли такие цифры подсунули в Москве или Питере. Скорее такой массовый этнузиазм проявили где-нибудь в провинции, где и наблюдателей толковых не было.

[kozlov]

Да, Аркадий, очень показательный график. Для меня, как человека с технической и математической подготовкой, никаких слов больше не надо. Все кристалльно ясно из графиков. Единая Россия, нарушив гауссово распределение, тем самым выдало себя с головой. Особенно бросается в глаза скачок с правой стороны кривой гауссианы. Кто же это так задорно рапортовал о 90-100% проголосовавших за ЕР? Врядли такие цифры подсунули в Москве или Питере. Скорее такой массовый этнузиазм проявили где-нибудь в провинции, где и наблюдателей толковых не было.

так и я о чем говорю. четкое и прямое доказательство

[Fantomas]

Все просто. Нет участков для выборов в конкретную партию. Избиратель идет голосовать по месту прописки. Получается пересечение двух множеств: множество избирателей (каждый со своими предпочтениями) случайно пересекается с множеством участков

Что значит мн-во избирателей пересекаецца с мн-вом участков? Образуецца новое мн-во (избирателей и участков)? И что это значит? Имхо, голосование на 1 участке не случайная величина. Сумма не случайных величин, имхо, тоже не случайная величина.

[Алексун Алексей]

Не даром Медведев назвал чурова волшебником

Сообщение отредактировал alexun: 10 December 2011 - 00:31

[Алексун Алексей]

http://www.ng.ru/politics/2011-12-09/3_nablyudatel.html